除以1.76目录

除以1.76的方法。
简介。
除以1.76在数学和工程应用中遇到的常见运算。有几种方法可以执行此操作,每种方法都有其优点和缺点。
手动除法。
手动除法是一种古老的方法,需要耐心和准确性。它涉及将被除数除以除数,然后将商写为商和余数。对于较大的数字,这种方法可以变得冗长且容易出错。
使用计算器。
使用计算器是除以1.76的一种快速且准确的方法。大多数计算器都具有除法键,可以自动执行此运算。为了获得精确的结果,请确保使用计算器的精度模式。
近似除法。
近似除法是一种估计商而非精确计算商的方法。一种常见的方法是在除数中找出最接近的因子。例如,1.76约等于1.8,除以1.8将产生近似商。这种方法可用于快速估计,但对于需要准确结果的应用不适合。
使用分数。
使用分数可以将除法转化为乘法。将除数表示为分数,然后将被除数乘以该分数的倒数。例如,要除以1.76,可以将其表示为176/100,然后将被除数乘以100/176。
应用示例。
除以1.76在许多应用中很有用,例如:。
计算平均值。
计算浓度。
转换单位。
进行财务计算。
结论。
有几种方法可以除以1.76,包括手动除法、使用计算器、近似除法和使用分数。选择哪种方法取决于所需的精度和便利性水平。
标签。
数学运算。
除法。
近似除法。
分数。
应用。
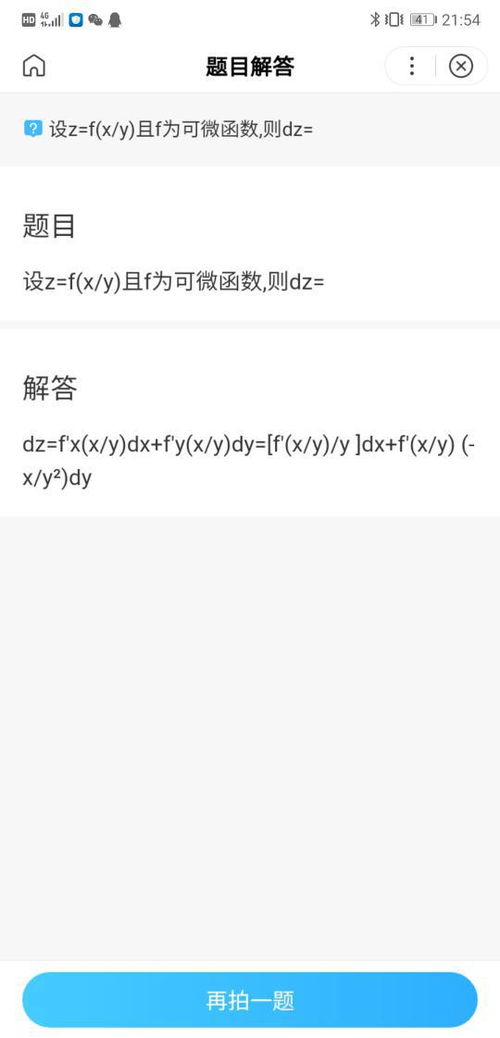
d2y除dx2怎么求?
什么是d2y除dx2?
d2y除dx2是指关于自变量x对y求二阶导数,然后再除以dx2。
求d2y除dx2的方法
要求d2y除dx2,需要对y关于x求一阶导数,然后再对一阶导数求导。表达式如下:
d2y/dx2=d(dy/dx)/dx
实例
例如,对于函数y=x2,求d2y除dx2:
一阶导数:dy/dx=2x
二阶导数:d2y/dx2=d(2x)/dx=2
因此,对于y=x2,d2y/dx2=2。
注意事项
在求d2y除dx2时,需要注意以下事项:
一定要先求一阶导数,然后再求二阶导数。
除数必须为dx2,而不是dx。
结果是一个常数、一个函数或另一个导数。
除以0.87和乘以1.13:有什么不同?
在数学运算中,除以一个数与乘以该数的倒数是等效的。在实际应用中,除以0.87和乘以1.13之间存在着微妙的区别,这可能会对结果产生影响。
除以0.87
除以0.87等于乘以1.149(0.87的倒数)。这可以表示为以下等式:
```
x÷0.87=x×1.149
```
除以0.87的作用是将数字缩小11.49。例如:
```
100÷0.87=114.94
```
这表示100除以0.87等于114.94,比原始数字大了14.94。
乘以1.13
乘以1.13等于除以0.87的倒数。这可以表示为以下等式:
```
x×1.13=x÷0.87
```
乘以1.13的作用是将数字增加11.49。例如:
```
100×1.13=113
```
这表示100乘以1.13等于113,比原始数字小11.49。
区别
除以0.87和乘以1.13之间的区别在于,除法会缩小数字,而乘法会增加数字。这意味着,如果数字最初大于1,除以0.87会得到更大的结果,而乘以1.13会得到更小的结果。反之亦然,如果数字最初小于1,除以0.87会得到更小的结果,而乘以1.13会得到更大的结果。
在实际应用中,这种区别可能会产生重大的影响。例如,在计算百分比变化时,使用除以0.87会得到一个较大的百分比变化值,而使用乘以1.13会得到一个较小的百分比变化值。
结论
除以0.87和乘以1.13等效的数学运算,但它们在实践中的作用却大不相同。除法会缩小数字,而乘法会增加数字。在计算百分比变化、财务分析和其他需要准确结果的应用中,了解这种差异非常重要。
标签
除法,乘法,比例,数学运算,百分比变化

1除以任何数等于多少?
理解除法概念
除法是一种数学运算,涉及将一个数字(被除数)分成相等的份数,并计算每个分数(商)的数量。当被除数为1时,除法的结果就是商。
1除以任何数的特殊情况
在数学中,当被除数为1时,除法具有一个特殊性质。无论除数是多少,1除以任何数的结果总是1。这是因为1是乘法单位,任何数字乘以1都不改变其值。
数学证明
我们可以通过数学证明来验证1除以任何数等于1。假设除数为x,那么:
```
1/x=(11)/x=1/x1=1
```
无论x的值是多少,等式始终成立,证明1除以任何数等于1。
实际应用
理解1除以任何数等于1的概念在实际应用中很有用,例如:
测量单位转换:如果1米等于100厘米,那么1厘米等于1米除以100,也就是1/100=0.01米。
百分比计算:如果代表总数,那么50代表总数的1/2,也就是1/2=0.5。
概率计算:如果抛一枚硬币,正面朝上的概率为1/2,也就是1除以抛硬币的可能结果数(正面和反面)。
结论
1除以任何数等于1是一个重要的数学概念,在各种领域都有实际应用。了解这个特殊情况可以帮助我们解决问题并理解数学运算。
标签
1除以任何数除法乘法单位数学概念实际应用
